The intuitive understanding of correlation coefficient
 |
| Photo by Dose Media on Unsplash |
Correlation is one of the statistics’ all-time classics, yet it is still a busy measure that everyone uses in their analysis process. In classic interpretation, correlation is a measure of relationship or correspondence between two variables. This is usually visualized through a correlation plot and measured using correlation coefficient (r) that ranges between -1 to 1. The important takeaway from r is it shows the degree of relationship between two variables in terms of how a change in one variable will lead to a change in the corresponding variable.
While interpreting the correlation plot is widely known and quite straightforward, the intuitive understanding of the equation of correlation coefficient (r) is less widely known. This is what the article is about. Why does the result be between -1 and 1; and where do the signs come from.
Before we continue to the explanation about r, let’s recall the definition of correlation.
Correlation: the relationship between two variables, indicating the probability that a change in one variable’s value will lead to a change in another variable’s values.
This is where r comes into play, it shows the degree of relationship between two variables. Sample’s correlation coefficient itself is calculated using the following formula:
Which can also be transformed into:
Let’s break down the equation.
The numerator of the equation is basically covariance measures, showing the relationship or the correspondence between the values of X and Y variables. The correspondence will tell us if the changes in the X variable’s values will bring a change in the Y variable’s values. Because of this reason, we want to make the values in X and Y variables comparable, hence we normalize the values by centering them, i.e. subtracting the values in X and Y variables with their mean (sample mean for sample, and population means for population).
Then centered values of X and Y variables are then multiplied which yields positive and negative values. Why is it so?
If the centered values in X and Y are both above and below the mean, the multiplication will yield positive values. If the values in X are above the mean and the values in Y are below the mean, the multiplication will yield negative values.
The summation ensures the balance of positive and negative values. It will yield to the direction of the changes between the corresponding X and Y variables. The product of the summation is then standardized by the corresponding standard deviation from X and Y variables. This ensures that the deviation of the values in X about their mean is proportional to the deviation of the values in Y about their mean. In the other words, this procedure ensures that the comparability of the values in X and Y variables.
Finally, the whole result is averaged by (n-1) (for a sample. For a population the result is divided with n).
The correlation coefficient (r) is therefore ranging between -1 to 1 because it is a product of a chain of mathematical procedures. The negative and positive signs are the products of the falling and rising of the values in variable X and Y. Correlation coefficient shows the strength of the relationship or correspondence between X and Y variables in a sense that a change in X variable’s values will lead to a change in Y variable’s values.
In conclusion...
The correlation coefficient (r) is a “normalized covariance” because the covariance between two variables is centered and standardized to ensure the comparability between the two variables. The degree of r that goes between -1 to 1 is the product of a chain of mathematical procedures. Positive and negative signs are the products of the combination of falling and rising in X and Y variables’ values. The correlation coefficient is then interpreted as a degree of relationship in the sense that a change in one variable will lead to a change in the corresponding variable.
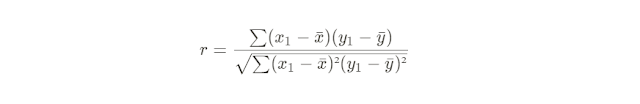




Comments
Post a Comment